Fluid mechanical kinematic optimization
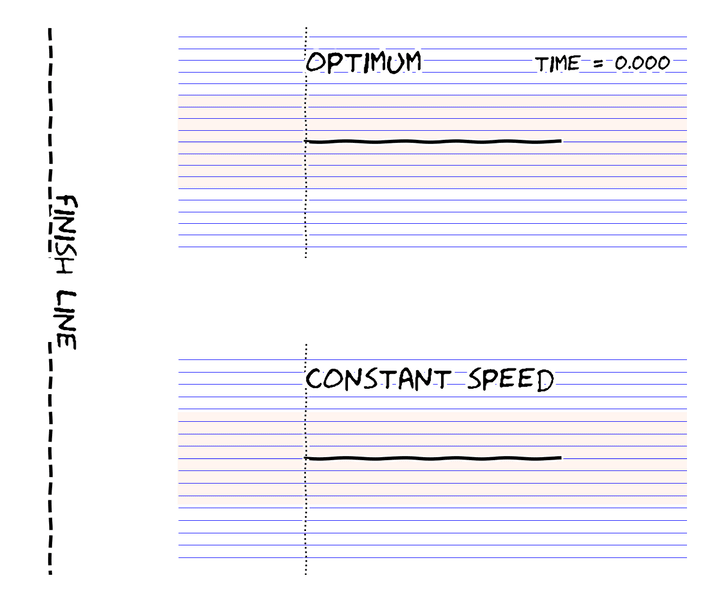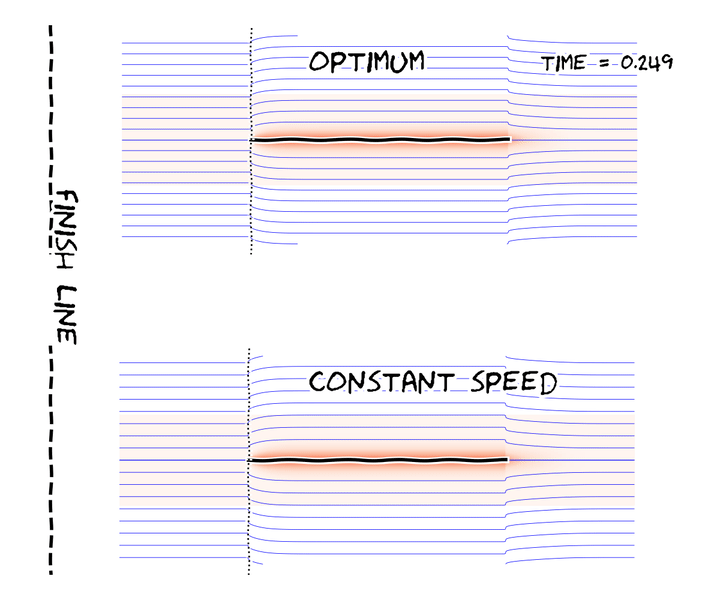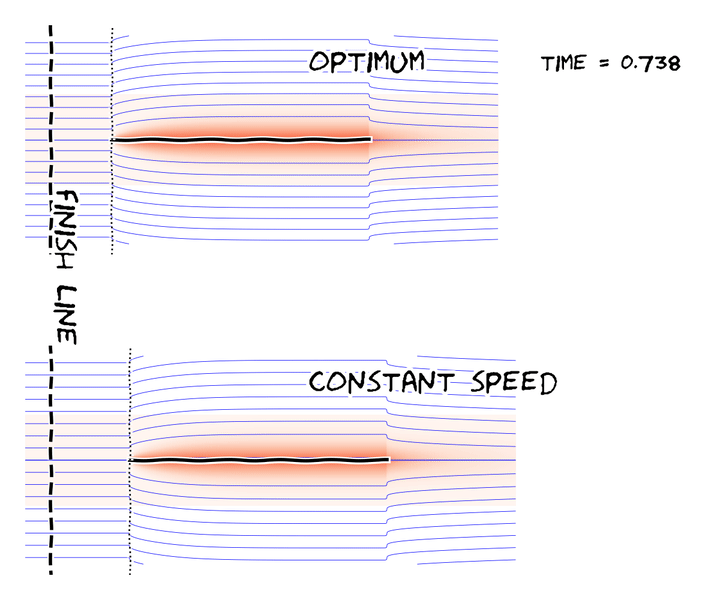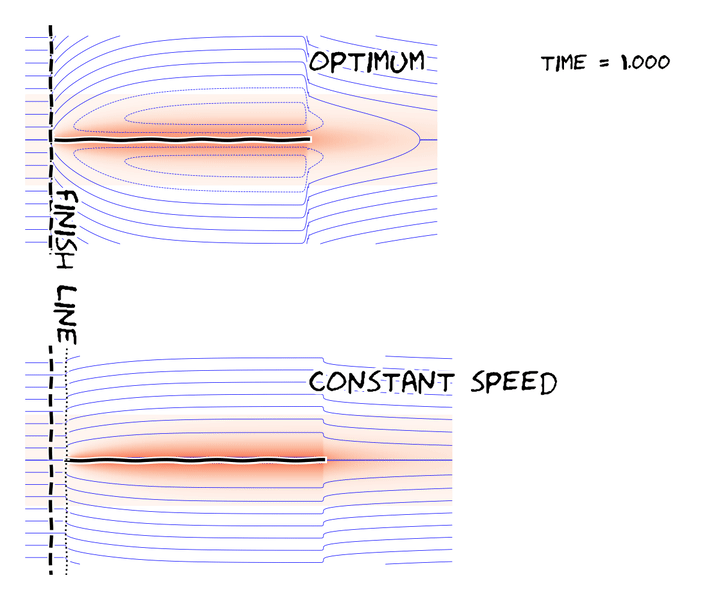
The fastest flat-plate under fixed energy budget Experimental demonstration of the classic brachistochrone. (credit: Technovation Projects) History of the brachistochrone featuring Prof. Steven Strogatz. (credit: 3Blue1Brown)
In 1696, Johann Bernoulli posed a challenge called the brachistochrone problem, which kickstarted the field of calculus of variations. Here is simplest fluid mechanical version of the brachistochcrone problem.
Johann Bernoulli’s challenge asked for the shortest time of travel between two points under gravity. For the fluid mechanical version, consider the minimum time it takes an object to move a given distance D in a fluid. Of course, the harder one can push the object, the faster it will move through the fluid. But suppose we insist that the mechanical work done in causing this motion to not exceed a given amount W. This problem shares its structure with many problems in bio- and bio-inspired robotic locomotion.
In one paper, we defined the fluid mechanical brachistochrone and found a rare analytical solution, which the adjoining figure shows.
Such an exercise furnishes much valuable insight into the structure of the optimum that compliments the rapidly developing ability of high-performance computers to compute them.
Publications
Mandre. Brachistochronous motion of a flat plate parallel to its surface immersed in a fluid. J. Fluid Mech., 939 A27 (2022).PDF Publisher link
Abstract: We determine the globally minimum time 𝑇 needed to translate a thin submerged flat plate a given distance parallel to its surface within a work budget. The Reynolds number for the flow is assumed to be large so that the drag on the plate arises from skin friction in a thin viscous boundary layer. The minimum is determined computationally using a steepest descent, where an adjoint formulation is used to compute the gradients. ... (read more)
Fluid mechanics Optimization Boundary LayersPDF Publisher link
Abstract: We consider the time-dependent speed of an infinitely long cylinder that minimizes the net work done on the surrounding fluid to travel a given distance perpendicular to its axis in a fixed amount of time. The flow that develops is two-dimensional. An analytical solution is possible using calculus of variations for the case that the distance travelled and the viscous boundary layer thickness that develops are much smaller than the circle radius. ... (read more)
Fluid mechanics Optimization Boundary Layers